| |
|
-
- Σ τ ο ι χ ε ῖ α
Β ι β λ ί ο ν αʹ
Π ρ ο β λ ή μ α τ α κ α ὶ
Θ ε ω ρ ή μ α τ α
- __________________________________________________
- γʹ Π ρ ό β λ η μ α
Δύο δοθεισῶν εὐθειῶν ἀνίσων ἀπὸ τῆς μείζονος
τῆι ἐλάσσονι ἴσην εὐθεῖαν ἀφελεῖν.
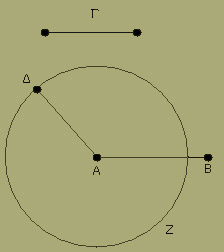
Ἔστωσαν αἱ δοθεῖσαι δύο εὐθεῖαι ἄνισοι αἱ ΑΒ, Γ, ὧν μείζων ἔστω ἡ ΑΒ· δεῖ δὴ ἀπὸ τῆς μείζονος τῆς ΑΒ τῆι ἐλάσσονι τῆι Γ ἴσην εὐθεῖαν ἀφελεῖν.
Κείσθω πρὸς τῶι Α σημείωι τῆι Γ εὐθείαι ἴση ἡ ΑΔ· καὶ κέντρωι μὲν τῶι Α διαστήματι δὲ τῶι ΑΔ κύκλος γεγράφθω ὁ ΔΕΖ.
Καὶ ἐπεὶ τὸ Α σημεῖον κέντρον ἐστὶ τοῦ ΔΕΖ κύκλου, ἴση ἐστὶν ἡ ΑΕ τῆι ΑΔ· ἀλλὰ καὶ ἡ Γ τῆι ΑΔ ἐστιν ἴση. ἑκατέρα ἄρα τῶν ΑΕ, Γ τῆι ΑΔ ἐστιν ἴση· ὥστε καὶ ἡ ΑΕ τῆι Γ ἐστιν ἴση.
Δύο ἄρα δοθεισῶν εὐθειῶν ἀνίσων τῶν ΑΒ, Γ ἀπὸ τῆς μείζονος τῆς ΑΒ τῆι ἐλάσσονι τῆι Γ ἴση ἀφήιρηται ἡ ΑΕ· ὅπερ ἔδει ποιῆσαι.
|
|