| |
|
-
- Σ τ ο ι χ ε ῖ α
Β ι β λ ί ο ν αʹ
Π ρ ο β λ ή μ α τ α κ α ὶ
Θ ε ω ρ ή μ α τ α
- __________________________________________________
- αʹ Π ρ ό β λ η μ α
Ἐπὶ τῆς δοθείσης εὐθείας πεπερασμένης
τρίγωνον ἰσόπλευρον συστήσασθαι.
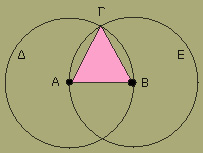
Ἔστω ἡ δοθεῖσα εὐθεῖα πεπερασμένη ἡ ΑΒ.
Δεῖ δὴ ἐπὶ τῆς ΑΒ εὐθείας τρίγωνον ἰσόπλευρον συστήσασθαι.
Κέντρωι μὲν τῶι Α διαστήματι δὲ τῶι ΑΒ κύκλος γεγράφθω ὁ ΒΓΔ, καὶ πάλιν κέντρωι μὲν τῶι Β διαστήματι δὲ τῶι ΒΑ κύκλος γεγράφθω ὁ ΑΓΕ, καὶ ἀπὸ τοῦ Γ σημείου, καθ' ὃ τέμνουσιν ἀλλήλους οἱ κύκλοι, ἐπὶ τὰ Α, Β σημεῖα ἐπεζεύχθωσαν εὐθεῖαι αἱ ΓΑ, ΓΒ.
Καὶ ἐπεὶ τὸ Α σημεῖον κέντρον ἐστὶ τοῦ ΓΔΒ κύκλου, ἴση ἐστὶν ἡ ΑΓ τῆι ΑΒ· πάλιν, ἐπεὶ τὸ Β σημεῖον κέντρον ἐστὶ τοῦ ΓΑΕ κύκλου, ἴση ἐστὶν ἡ ΒΓ τῆι ΒΑ. ἐδείχθη δὲ καὶ ἡ ΓΑ τῆι ΑΒ ἴση· ἑκατέρα ἄρα τῶν ΓΑ, ΓΒ τῆι ΑΒ ἐστὶν ἴση. τὰ δὲ τῶι αὐτῶι ἴσα καὶ ἀλλήλοις ἐστὶν ἴσα· καὶ ἡ ΓΑ ἄρα τῆι ΓΒ ἐστὶν ἴση· αἱ τρεῖς ἄρα αἱ ΓΑ, ΑΒ, ΒΓ ἴσαι ἀλλήλαις εἰσίν.
Ἰσόπλευρον ἄρα ἐστὶ τὸ ΑΒΓ τρίγωνον, καὶ συνέσταται ἐπὶ τῆς δοθείσης εὐθείας πεπερασμένης τῆς ΑΒ. [Ἐπὶ τῆς δοθείσης ἄρα εὐθείας πεπερασμένης τρίγωνον ἰσόπλευρον συνέσταται]· ὅπερ ἔδει ποιῆσαι.
|
|